2023. 7. 25. 11:31ㆍ주식
안녕하세요
주식하는 소녀입니다.
분식회계를 잡아낼 수 있는 마법같은 법칙이 있습니다.
바로 그것은... 두규두규두규~!!!
Benford's Law
벤포드의 법칙이라는 것인데요
오늘은 벤포드의 법칙에 대해서 간단히만 알아보고,
다음 편에서 이어질 본론에서는 제가 오랫동안 공을들인,
주식시장에의 적용을 통한 예측!! 을 이야기해보도록 하겠습니다.
(기대해주쎄용)

데이터 세상이라고하죠
세상에 존재하는 이 수많은 숫자들 가운데
10진법 세상에서 첫자리 숫자는 무엇이 많을까유?
첫자리 숫자란: eg. 1(1이 첫자리숫자) 564(5가첫자리숫자) 878(8이 첫자리 숫자)
당연히!! 1부터 9까지 무작위니까 1~9 9가지 숫자가 각자 11%씩 나눠가질거라고 대답하는게 일반적인 상식일 것입니다.
하지만 실제로는 그렇지 않습니다
‘1’이 가장 높은 비율, 그다음이 ‘2’, 다음이 ‘3’ 등으로 비율이 순서대로 낮아지며
이것을 ‘벤포드의 법칙’이라고 말한답니다.
이게 뭔소리냐고요??????
놀랍게도 사실입니당 ㅠㅠ
이 법칙은 1938년 미국의 물리학자 프랭크 벤포드가 발표하면서 그의 이름을 따 붙었다. 하지만 그에 앞서 미국 천문학자 사이먼 뉴컴이 1881년 먼저 이런 경향을 언급한 바 있다. 벤포드는 20개의 서로 다른 데이터셋들을 비교한 결과, 모두 시작 숫자의 비율이 희한하게 비슷하다는 점을 발견했다. 대상에는 335개 강의 표면적, 104개의 물리학 상수, 1800개의 분자 무게, 5000개의 수학책에 나오는 숫자, 308개의 잡지 <리더스 다이제스트>에 나오는 숫자 등이 포함됐다. 조사 결과 놀랍게도 이 데이터에 등장하는 첫 번째 숫자의 비율은 모두 다음과 비슷하게 나타났다. (출처: hani.co.kr/arti/science)
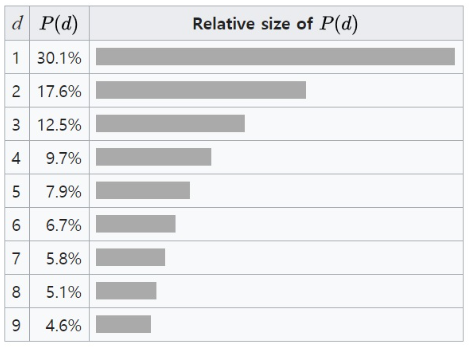
자 어떤가요
벤포드의 법칙.. 신기하지 않나요?

8,000원 대의 주식이 9,000원으로 넘어가는게 빠르다면
이를 우린 흥미롭게 쳐다볼 수 있겠죠잉~~
주식 가격에 적용이 어렵다면,
거래량에는 적용이 가능할지 예측이 가능할지 살펴봐도 좋을 것 같구요.
최소한, 벤포드의 법칙을 잘 관찰해두면,
투자를 결정하는 수많은 근거와 툴 중 하나로
매우 유용하게 사용해볼 수 있지 않을까 싶네요.
그럼 우리는 다음시간에 더 유용한 정보로 만나요~~
좋으셨으면 댓글과 구독 갑시당!!

'주식' 카테고리의 다른 글
| 국내 상장된 미국 국채 ETF 가 추종하는 기초지수 내용 알아보기 (Bloomberg US Treasury 20+ Year Total Return, S&P Ultra T-Bond Futures Excess Return Index) (0) | 2023.07.27 |
|---|---|
| 미국 국채 ETF 상세 비교 (증권사수수료 / 환헷지 여부) (0) | 2023.07.26 |
| PMI (구매자관리지수) 지표란? (2) | 2023.07.20 |
| Self retrospect (230717) (0) | 2023.07.19 |
| 엔화 예금통장 만들기 (0) | 2023.07.18 |